Difference between revisions of "TagesLaenge"
From Dietrich Blog (Strato)
(→Die Formel) |
(→Die Formel) |
||
| Line 8: | Line 8: | ||
<math>\cos t = -( \tan \phi * \tan \delta ) </math> | <math>\cos t = -( \tan \phi * \tan \delta ) </math> | ||
<br />Wobei: | <br />Wobei: | ||
| − | + | ;t:halber Tagesbogen | |
| − | + | ;φ (phi):Geografische Breite | |
| − | + | ;δ (delta):Deklination der Sonne | |
| − | |||
| − | |||
Die Deklination der Sonne können wir vereinfacht berechnen als (Quelle: http://lexikon.astronomie.info/zeitgleichung/): | Die Deklination der Sonne können wir vereinfacht berechnen als (Quelle: http://lexikon.astronomie.info/zeitgleichung/): | ||
<pre> | <pre> | ||
Revision as of 14:57, 13 November 2008
Siehe auch: Astronomie, Collected Excel Sheets
Die Formel
Dafür habe ich als Schüler folgende Formel gefunden:
cos t = -(tan(φ) * tan(δ))
<math>\cos t = -( \tan \phi * \tan \delta ) </math>
Wobei:
- t
- halber Tagesbogen
- φ (phi)
- Geografische Breite
- δ (delta)
- Deklination der Sonne
Die Deklination der Sonne können wir vereinfacht berechnen als (Quelle: http://lexikon.astronomie.info/zeitgleichung/):
delta = 0.40954*sin(0.0172*(T-79.35))
Wobei:
- T:
- Tagesnummer im Jahr; d.h. der erste Januar hat die Nummer 1, der zweite Januar die Nummer 2 usw.
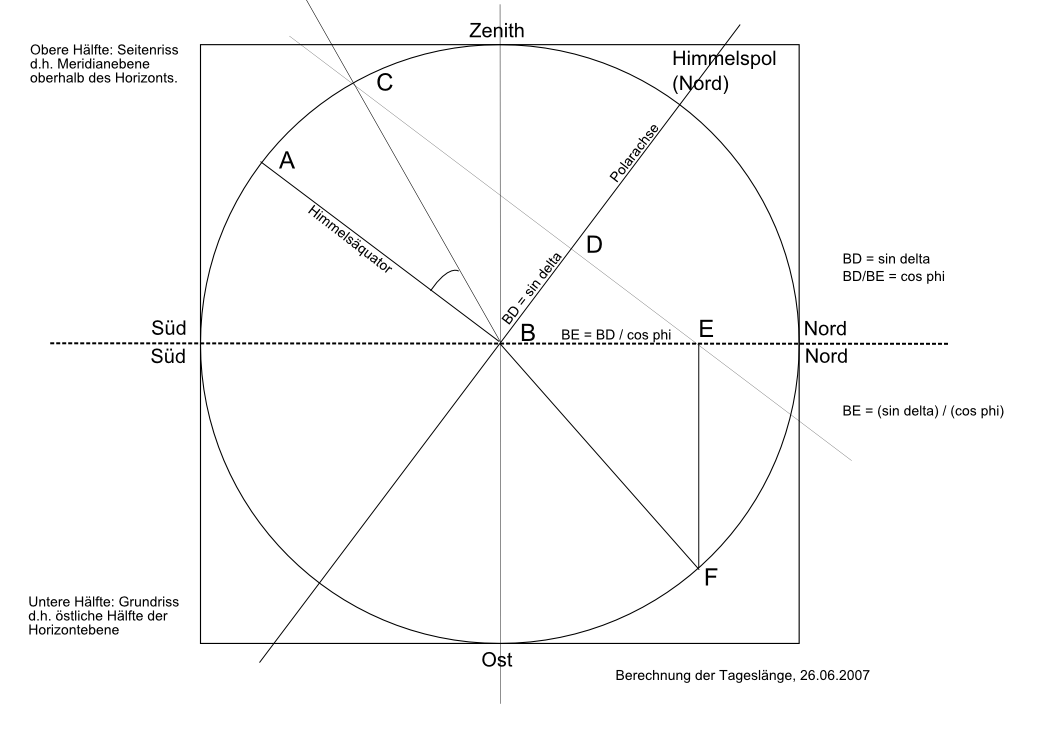
Die Zeichnung
-- Main.DietrichKracht - 19 Mar 2005